Conceptual design of a DNA catch bond
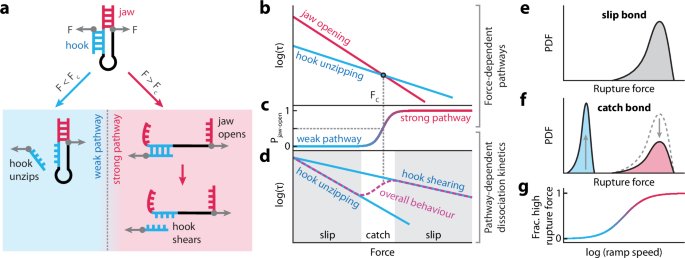
To create a catch bond, our strategy is to design a DNA construct with two dissociation pathways of distinct mechanical strengths. By biasing towards the weak pathway at low force and the strong pathway at high force, we can effectively create the catch behaviour. To do so, we designed a force-switchable structure with two rupturable domains, nicknamed the hook and the jaw (Fig. 1a). When force is initially applied at the two points, both the hook and jaw are in the unzipping geometry and compete to unbind. If the hook opens first, the closed jaw locks it in the weak unzipping geometry. On the other hand, if the jaw opens first, the hook converts to the stronger shearing geometry. We have accomplished our goal if we can predictably control which of the two pathways is active by force. Our previous work demonstrated that the unzipping of two DNA placed in series can be preferentially controlled by force and sequence (Supplementary Fig. 1)42. Thus, we designed the jaw and hook sequences such that the τF of jaw unzipping is higher than hook unzipping at low force and vice versa at high force, intersecting each other at a crossover force (Fc) (Fig. 1b). The differential unzipping τF ensures that the hook is more likely to open at F < Fc. In contrast, the jaw is more likely to open at F > Fc, effectively creating a force-dependent bias towards the weak and strong pathways around Fc (Fig. 1c). Given that the ultimate hook dissociation in the weak and strong pathways are unzipping and shearing, respectively, the switching from the weak pathway to the strong pathway as force increases will effectively create a slip-catch-slip behaviour (Fig. 1d).
Fig. 1: Schematics of DNA catch bond design and expected behaviour.
a Schematic of a two-state mechanism that allows the DNA construct to dissociate via two pathways directed by force above or below a crossover force (Fc). In the weak pathway, the closed jaw locks the hook in the unzipping geometry. In the strong pathway, the open jaw switches the hook to the shearing geometry. b The lifetimes (τF) of the hook unzipping and jaw opening are designed to intersect, enabling force-dependent pathway selection. c Below Fc, the construct follows the weak pathway, as the jaw remains closed, and thus the hook unzips. Above Fc, the jaw opens before the hook, steering the construct into the strong pathway, thereby increasing the proportion of constructs with an open jaw (Pjaw-open) as force escalates. d As the force increases, the transition from the hook unzipping to shearing creates a slip-catch-slip behaviour. e Slip bonds are characterized by a unimodal rupture force probability density function (PDF) at a specific loading rate. f In contrast, catch bonds exhibit a bimodal rupture force PDF (catch-slip-catch shown here). Here, the high rupture force population (red) corresponds to high-force slip behaviour and the low rupture force population (green) arises from the catch behaviour. For comparison, a slip-only PDF is represented by a grey dashed line. The catch behaviour shifts subpopulations from high-force to low-force ruptures (grey arrows). g Additionally, the fraction of high rupture force in the bimodal distribution increases with force ramp speed or loading rate.
Relating our system to the two-state, two-pathway model, the weak, closed-jaw conformation is Sw, while the strong, open-jaw conformation is Ss. The conversion rates between Sw and Ss are the unbinding and rebinding rates of the jaw hairpin, which are slow due to the large loop. This slow conversion rate is characteristic of the two-state model and is necessary to explain the catch-slip behaviour of FimH/mannose24, vinculin/F-actin8, and cadherins in the X-dimer configuration11. At faster conversions, the two-state model collapses to the one-state model12, which assumes a single bound state with two competing unbinding pathways12,15,39,41. The survival probabilities predicted from the one-state model fit catch-slip data collected from P- and L-selectins/PSGL-112,15 and myosin/actin43. This general framework for building an artificial catch bond aligns with the guiding principles described earlier10,31,32,33.
The force-dependent dissociation of interactions can be experimentally examined by SMFS. The rupture force distributions in a force ramp experiment provide the mechanical signatures of the bond characteristics. For a slip bond, the dissociation probability monotonically increases with force over time until the cumulative dissociation probability approaches 1, leading to a unimodal rupture force distribution (Fig. 1e). However, for a slip-catch-slip bond, the local minimum in τF creates a local maximum in dissociation probability, resulting in an additional peak in the rupture force distribution. This bimodal distribution is the first signature of a catch bond (Fig. 1f). Additionally, the force ramp speed controls the population ratio of the bimodal rupture force distribution, with higher ramp speed biasing towards more high-force ruptures (Fig. 1g). This force-dependent ratio of the two rupture force populations is a second signature of a catch bond.
Characterization of the DNA catch bond by SMFS
To implement the above strategy, we created a fish and a hook, two DNA pieces that act as receptors and ligands in this artificial catch bond. In our dual trap optical tweezers experiment, the hook was bound to one bead and the fish to the other (Fig. 2a). With this configuration, we began an approach-dwell-retract fishing pattern where the fish bead would approach the hook, dwell for a few seconds, and then retract. The fish contains a closed jaw and a single-stranded region complementary to the hook (Fig. 2a, b – regrettably, the jaw does not bite the hook). In order to show the two signatures of a catch bond (Fig. 1f, g), we designed the hook and jaw sequences by considering the ramp speed limits of our optical tweezers (max 2000 nm s−1). We used an analytical model to find τF for sequences of various lengths and CG contents, and then used Monte Carlo simulations that emulate our pulling experiments to find a set of sequence parameters that would show a clear shift towards high-force rupture population at our available ramp speeds. Further details about the model and simulation can be found in the Methods section. The construct we selected has a jaw length of 18 base pairs (bp), of which 8 are C/G (jaw 8/18); and a hook length of 9 bp, of which all 9 are C/G (hook 9/9). (Fig. 2b) This construct is predicted via the analytical model to have the slip-catch-slip τF shown in Fig. 2d with an Fc of 12.6 pN. To ensure the jaw can open fully, the loop must be at least as long as the two jaw strands combined; in our case, our jaw was 18 bp long, so the loop must be at least 36 nucleotides (nt) (Fig. 2b). We designed the poly-T section of the loop to be 42 nt long as an extra precaution.
Fig. 2: Experimental setup and catch bond sequence design.
a Schematic representation of the dual-trap optical tweezers experiment. The hook is attached to bead A, and the fish is attached to bead B via DNA handles of 2633 and 272 bp, respectively. Both handles are attached to the beads by a biotin-streptavidin linkage on the 5′ end of each handle (top inset). Bead B undergoes an oscillatory motion with a dwell period before retraction (bottom inset) to increase the fishing success rate (binding between the hook and the fish). b The construct sequence. A 9-mer polyethylene glycol (PEG) linker attaches the hook to its DNA handle to minimize nonspecific base interactions with the fish and increase flexibility. c Schematic showing the weak and strong pathways. d The expected τF of the selected construct sequence based on our analytical model, showing the overall expected slip-catch-slip behaviour resulting from transitioning from hook unzipping to hook shearing around the intersection of the jaw opening and the hook unzipping τF at Fc = 13.6 pN. The anticipated force-extension curves differ for the weak (e) and strong (f) pathways, as predicted by the extensible worm-like chain model (XWLC). In the weak pathway, we expect a singular low-force rupture event indicative of hook unzipping (e). In the strong pathway, we expect a jaw-opening transition preceding a high-force rupture event corresponding to hook shearing (f).
Once the hook successfully catches the fish, it will unbind via one of the two pathways (Fig. 2c). In the weak pathway (F < Fc), the hook unzips first, leaving a low rupture force signature characteristic of DNA unzipping (Fig. 2e). Conversely, in the strong pathway (F > Fc), the jaw opens before the hook unbinds, creating an unfolding event with a change in contour length (ΔLc) corresponding to the loop size. As the force continues to increase, the hook, now in the shearing geometry, will eventually rupture at a much higher force (Fig. 2f). The two pathways can be clearly distinguished by examining their force-extension signatures. If the system undergoes the weak pathway, the fish remains folded in the original conformation with its jaw closed. If the system undergoes the strong pathway, the jaw will remain open until the hook unbinds but will refold and revert to its initial jaw-closed conformation. Hence, the fish-hook catch interaction can be indefinitely repeated.
In the fishing experiment, we pulled every tether until it broke to ensure both a single tether interaction and a new fish-hook pair formed each time. The force-extension curves showed two distinct behaviours: a population of curves that break at low forces (10–15 pN), corresponding to hook unzipping in the weak pathway (Fig. 3a, blue traces), and another population of curves that break at high forces (30–50 pN), corresponding to hook shearing in the strong pathway (Fig. 3a, red traces). The latter is always accompanied by an additional low force (10–15 pN) unfolding event prior to rupture with a contour length difference (ΔLc) of 20.4 ± 0.3 nm, which is in excellent agreement with the theoretical ΔLc of 20.2 nm (Fig. 3b) of the jaw-opening event in the strong pathway. Additionally, the force-extension curves of the weak pathway align with the pre-rupture portion of the strong pathway, indicating both are in the jaw-closed conformation. This evidence demonstrates that the fish-hook system exhibits the two designed pathways. We used an approach-dwell-retract fishing pattern to maximize the likelihood of catching a fish on any given approach (Fig. 2a, inset). The dwell time of ~8 s allowed the 9 bp hook to find a fish reliably while also allowing any fish with open jaws from the previous pull to close their jaws, preventing any history-dependent behaviour. We tested multiple beads in multiple samples for each experimental condition.
Fig. 3: Experimental and simulation results from the optical tweezers.
a Experimental force-extension curves in chronological order from a medium ramp experiment, showing non-history dependent switching between strong (red) and weak (blue) rupture events for the hook9/9-jaw 8/18 construct shown in Fig. 2b. Traces end when the hook unbinds. Fishing attempts that do not yield single tethers are not shown. b The same force-extension curves in (A), but with theoretical worm-like chain curves overlaid for the two possible states (dashed lines). The distribution of ΔLc (inset) from all medium pulls with a jaw opening event, as compared with the theoretical ΔLc of 20.20 nm. c Rupture force distributions at three pulling rates compared to the Monte-Carlo simulation. The slow pulling rate has a higher proportion of hook unzipping, while the fastest pulling rate has a higher proportion of hook shearing. d Rupture force plotted against force loading rate for the three ramps, calculated at the moment of rupture. Due to the long DNA handles, each pulling speed (nm s−1) has a range of loading rates (pN s−1) obtained from the worm-like chain model. e The proportion of open-jawed constructs as a function of pulling rate compared to the simulation. Two additional catch bonds were tested in addition to the one shown in the rest of Figs. 2 and 3 (h9/9j8/18), one with an 11/11 CG content hook (h11/11j8/18; yellow; n = 101, 178, 130 for slow, medium, and fast ramp speed) and one with a 10/18 CG content jaw (h9/9j10/18; green; n = 253, 490, 187 for slow, medium, and fast ramp speed). Error bars are the 95% confidence interval of the proportion; n = 1000 for each simulated point.
Next, we examined the rupture force distribution of the fish-hook catch bond at fast (2067 nm s−1), medium (206.7 nm s−1), and slow (51.7 nm s−1) ramp speeds (Fig. 3c). In all three experimental sets, the fish-hook system exhibits the characteristic bimodal distribution of a catch bond. By checking for the presence of a jaw-opening event, we are able to determine the dissociation pathway and colour code them in the histograms, where the lower force peak is dominated by the weak hook unzipping pathway, while the high force peak is dominated by the strong hook shearing pathway. Our simulation of the system demonstrates quantitatively similar bimodal distribution as the experiment, taking into account the non-linear elasticity of the DNA handles in the optical tweezers experiment. To examine this further, we plotted rupture force as a function of the loading rate at the time of rupture, colour-coded by the identity of the pathway (Fig. 3d). As expected, the rupture forces from both pathways increase with ramp speed and loading rate. The simulated results under the same conditions overlayed well with the experimental results. The scatter distribution from each ramp speed is curved due to the non-linear elasticity of the DNA handle used in the optical tweezer experiment, where the loading rate (pN s-1) scales with the spring constant (pN nm-1) at constant ramp speeds (nm s−1).
Lastly, we examined the fraction of rupture events undergoing the strong and the weak pathways at different ramp speeds. The fraction of rupture events from the strong pathway increased from 0.33 at the low ramp speed to 0.74 at the fast ramp speed (Fig. 3e, pink). This, again is in good agreement with our simulation results indicating that higher ramp speed leads to a greater fraction of rupture events from the strong pathway (Fig. 3e), demonstrating our fish-hook system exhibits the designed catch bond behaviour. Our experimental results cover approximately 2 orders of magnitude in ramp speed, which are at the limit of our instrument (high ramp speed) and reasonable experimental time scale (low ramp speed). We additionally tested 2 other fish-hook catch bonds, one with a longer hook (Fig. 3e, yellow, CG content of 11 bp, length of 11 bp (11/11 hook)) and one with a more CG-rich jaw (Fig. 3e, green, CG content of 10 bp, length of 18 bp, (10/18 jaw)). The longer hook resulted in a higher proportion of jaw-opening at the same speeds. This makes sense because a longer hook is a stronger hook, making the jaw weaker by comparison and allowing it to open more often. The opposite is true of creating a more CG-rich jaw: if the jaw is stronger, the hook unzips more often, shifting the proportion of jaw opening events down at the same speeds. As with the original fish-hook, these trends are mirrored by the model.
Design of fish-hook catch bonds in biological ranges
The design space of the fish-hook catch bond is vast. Using the analytical model, we searched all hook/jaw sequence combinations with varying CG contents and lengths from 7–30 bp for catch behaviour. For a combination to have catch behaviour, the following conditions must be met: First, the log(τF) curves of the hook and jaw must intersect. The intersection creates the force-dependent state switching behaviour and dictates the force range (around Fc) at which it happens. Second, the log(τF) curves of the hook and jaw must intersect in the correct order: the τF of the hook must be lower than the jaw at lower force and higher than the jaw at higher force. In other words, the slope of log(τF) for the jaw must be steeper than the hook. In the opposite case, the hook would shear at low force and unzip at high force, leading to a more exaggerated slip behaviour rather than slip-catch-slip. The slope of log(τF) in hairpin unzipping is almost entirely dependent on the sequence length, rather than CG content42, thus the jaw should be longer than the hook. Third, there must exist a positively-sloped (catch) region in the overall log(τF). Even if the hook and jaw intersect correctly, the overall τF may not have a catch region for two reasons: Firstly, when the slopes of the hook and jaw are very similar, the state switching from hook unzipping to shearing occurs too gently for log(τF) to be positively sloped. Secondly, as Fc approaches 0, the difference between the shearing and unzipping log(τF) of the hook is less prominent and disappears at F = 0, thus reducing both the height and width of the catch region.
Within these bounds, we found 96645 combinations satisfying the first two conditions; of those, 54354 had a positively-sloped catch region (Supplementary Figs. 4, 5); of those, 3493 were within a biologically relevant range (we define this as τF in the catch region between 0.01–100 s and the force marking the start of catch region (Fstart) between 0-10 pN). We found τF located at Fstart and Fend (Fig. 4d) for the catch region of each construct (Fig. 4a) and calculated the force range (ΔF) and τF range (Δlog(τF)) that characterize the catch region of each construct (Fig. 4b). Both graphs (Fig. 4a, b) are colour-coded by the 2D colormap shown in the inset of Fig. 4b.
Fig. 4: Fish-hook catch bond design space.
a Catch regions of fish-hook catch bonds within the biologically relevant window of 0.01 <τ < 100 s and 0 <Fstart < 10 pN, simplified to a straight line between the lowest and highest τF. The tallest and widest catch behaviours are marked with * and #, respectively. b The characteristic Δlog(τF) and ΔF parameters of the catch regions. c, d The tallest and widest catch regions from (a, b). e Jaw lengths and CG contents that create catch behaviour are shown, coloured by the number of hook sequences that form catch bonds with them. The most versatile jaw, with a 0 bp CG content and a 27 bp length of (jaw0/27), is marked by a black box. f The hook sequence space that forms catch behaviour with the most versatile jaw in (e). g, h The same as (e, f), but for the hook design space and the jaws, which catch with the most versatile hook, which has an 8 bp CG content and an 8 bp length (hook8/8). Colours in (a–d, f, h) are coded by the 2D colour bar of the (b) inset.
We see a vast diversity of behaviours even in this biologically-relevant subset of the total design space, with catch behaviour covering up to two orders of magnitude in τF and up to 8 pN in ΔF (Fig. 4b). The τF of the constructs exhibiting the greatest Δlog(τF) and ΔF are shown in Fig. 4c, d, and marked by * and #, respectively in Fig. 4a, b. One interesting feature of the design space in Fig. 4b is the abundance of quasi-ideal bonds covering the bottom of the fin-shaped distribution with relatively small changes in τF (« 1 order of magnitude). Outside of this quasi-ideal bond range, there is a distinct lack of steep catch bonds with narrow force ranges (ΔF < ~ 3 pN) to the left edge of the fin (Fig. 4b). This is because ΔF depends on how different the slopes of hook unzipping τF and jaw opening τF are. If they are very different, ΔF is very narrow – the extreme case where jaw opening is perfectly vertical and hook unzipping is perfectly horizontal would have a ΔF of 0. Since a DNA unzipping slope can only be so different from another DNA unzipping slope, DNA will never be able to probe this area of catch behaviour alone42. That said, one can imagine that by constructing the hook or jaw with biomolecular interactions other than DNA unzipping, more of this area could be covered.
Next, we explore the combinatorial sequence space of jaw and hook that creates catch bond behaviour within the biologically relevant range as defined earlier. We found that the most versatile jaw had a length of 27 bp made entirely of A/T (Fig. 4e) and can create catch behaviour with 44 unique hooks from 7–19 nt with relatively low CG content (Fig. 4f). The most versatile hook had a length of 8 bp made up entirely of C/G (Fig. 4g) and can create catch behaviour with 124 unique jaw sequences between 13–30 nt also with relatively low CG content (Fig. 4h). The fact that the most versatile lengths are near the upper and lower extremes of our search space highlights the fact that length changes the slope of the log(τF) – the steeper slope (longer sequence) the jaw has, the more hooks it pairs with; and the flatter slope (shorter sequence) the hook has (Supplementary Fig. 1), the more jaws it pairs with. CG content represents a vertical shift in log(τF), which also makes sense with the most versatile jaw/hook42: as the jaw CG content decreases or the hook CG content increases, Fc increases and a more dramatic catch behaviour is observed due to a larger difference in shearing and unzipping τF.